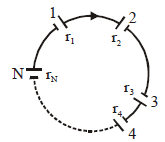
Solution:

In the given circuit of $N$ cells, the emf ($E_N$) and internal resistance ($r_N$) are related as $E_N = 1.5r_N$. To find the current ($I$), we follow these steps:

1. Equivalent emf and resistance:
   • The cells are connected in series, so: $$E_{\text{eq}} = E_N = 1.5r_N, \quad r_{\text{eq}} = r_N.$$
2. Total resistance:
   • Let $R_{\text{ext}}$ be the external resistance of the circuit. From the figure, the circuit resistance is: $$R_{\text{total}} = r_N + R_{\text{ext}}.$$
3. Ohm's Law:
   • The current in the circuit is: $$I = \frac{E_{\text{eq}}}{R_{\text{total}}} = \frac{1.5r_N}{r_N + R_{\text{ext}}}.$$
4. Condition for ( I = 1.5 , \text{A}:
   • Substituting $I = 1.5$ into the equation:

     $$1.5 = \frac{1.5r_N}{r_N + R_{\text{ext}}}.$$

   • Simplifying:

     $$r_N + R_{\text{ext}} = r_N \implies R_{\text{ext}} = 0.$$

Thus, the current $I = 1.5 \, \text{A}$ when $R_{\text{ext}} = 0$, meaning there is no external resistance.