Solution:

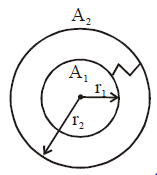
The problem involves two spherical conductors $A_1$ and $A_2$ connected by a copper wire. Let’s analyze and compute the equivalent capacitance of the system.

Given:

• $A_1$ and $A_2$ are concentric spherical conductors.
• Radii of the spheres: $r_1$ (inner) and $r_2$ (outer).
• The medium is air, so the permittivity is $\varepsilon_0$.

Key Concepts:

1. Potential Difference Between the Spheres: The two conductors are connected by a wire, meaning they are at the same potential. As a result, the electric field exists only between the two spheres.
2. Capacitance of a Single Isolated Sphere: If only $A_2$ existed as a spherical conductor, its capacitance would be:

   $$C_{\text{single}} = 4 \pi \varepsilon_0 r_2.$$

3. Why the System is Equivalent to an Isolated Sphere: Since $A_1$ is connected to $A_2$ via a conducting wire, any charge added to $A_1$ immediately flows to $A_2$, making the system behave as if there is only one conductor of radius $r_2$.

Equivalent Capacitance:

Thus, the capacitance of the system is:

$$C_{\text{equivalent}} = 4 \pi \varepsilon_0 r_2.$$

Final Answer:

The equivalent capacitance of the system is:

$$\boxed{4 \pi \varepsilon_0 r_2}.$$