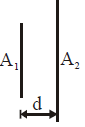
Solution:

The capacitance of a parallel-plate capacitor is given by the general formula:

$$C = \frac{\varepsilon_0 A}{d}$$

where:

• $C$ = capacitance,
• $\varepsilon_0$ = permittivity of free space,
• $A$ = effective overlapping area of the two plates,
• $d$ = separation between the plates.

For Plates of Unequal Areas ($A_1 < A_2$):

When two plates of areas $A_1$ and $A_2$ are used to form a capacitor, only the smaller area ($A_1$) determines the effective overlapping area for charge storage. This is because the excess area of the larger plate ($A_2 - A_1$) does not contribute to the capacitance.

Thus, the capacitance is:

$$C = \frac{\varepsilon_0 A_1}{d}$$

Final Answer:

The capacitance of the capacitor is:

$$\boxed{C = \frac{\varepsilon_0 A_1}{d}}$$