A 2μF capacitor is charged as shown in figure. The percentage of its stored energy dissiplated
after the switch S is turned to position 2 is :
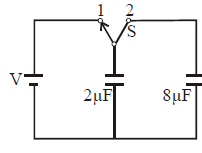
Solution:
To solve this, let's calculate the percentage of energy dissipated when the switch is turned to position 2.
Given:
- Initial voltage across
Key Concept:
When two capacitors are connected, the redistribution of charge causes energy loss. The energy dissipated can be calculated using the direct formula:
Here:
- is the initial voltage of .
- (initially, is uncharged).
Step-by-step Calculation:
- Common Voltage after Connection: The final voltage across both capacitors is:
- Initial Energy Stored in :
- Final Energy Stored: The total energy stored after redistribution is:
Substituting values:
- Energy Dissipated:
- Percentage of Energy Dissipated:
Final Answer:
The percentage of energy dissipated is 80%.

Leave a Reply