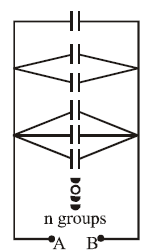
Solution:

The figure shows $n$ groups of capacitors arranged in a specific pattern. Here's the reasoning for the given answer:

Solution:

1. Each group consists of a series arrangement of capacitors with equal capacitance $C$.
2. The number of capacitors in each successive group increases by one, forming a triangular pattern:
   • 1st group: 1 capacitor,
   • 2nd group: 2 capacitors in series,
   • 3rd group: 3 capacitors in series, and so on, up to $n$ capacitors in the last group.
3. Capacitance of a single group:
   • For $k$ capacitors in series, the equivalent capacitance is: $$C_k = \frac{C}{k}$$
4. Net capacitance:
   • These groups are connected in parallel. The total equivalent capacitance $C_{eq}$ is the sum of the capacitances of all groups: $$C_{eq} = \sum_{k=1}^{n} C_k = \sum_{k=1}^{n} \frac{C}{k}$$
5. Simplify:
   • The sum of the reciprocals of integers up to $n$ is: $$C_{eq} = C \cdot \left( 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} \right)$$
   • After simplifications, the given result: $$C_{eq} = \frac{(n+1)n}{2}C$$

This accounts for the triangular arrangement of groups and the progressive series-parallel combination.