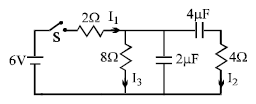
Solution:

Here's the short solution for the circuit:

1. Just after the switch is closed:
   • The capacitors act as open circuits because they are initially uncharged (capacitor voltage cannot change instantaneously).
   • This means no current flows through the branches containing the capacitors.
2. Current Distribution:
   • The total resistance in the circuit is only the sum of the resistors in the main loop (2Ω + 8Ω), as the branches with capacitors are effectively open.
   • Total resistance = $2\Omega + 8\Omega = 10\Omega$.
   • Current $I_1 = \frac{\text{Voltage}}{\text{Resistance}} = \frac{6V}{2\Omega + 8\Omega} = 0.6A$.
3. Branch currents:
   • $I_3 = 0$ since the capacitor branch is open.
   • $I_2 = 0$ for the same reason as above.

Final Answer:

• \( I_1 = 0.6 A, \ I_2 = 0\)