Solution:

The heat absorbed during the fusion process is given by the formula:

\[
H = m \cdot L
\]

Where \( H \) is the heat absorbed, \( m \) is the mass, and \( L \) is the latent heat of fusion. Since both substances have the same mass and are being heated at the same rate (6 cal/s), the amount of heat absorbed depends on the duration of the phase change (the flat portion of the graph).

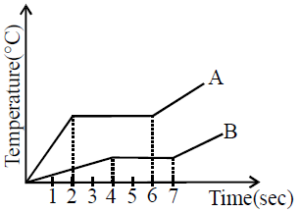
- For substance A: The time interval for fusion (flat portion of the graph) is from \( t = 3 \) to \( t = 5 \), so the time spent during fusion is \( 5 - 3 = 2 \) seconds.
- For substance B: The time interval for fusion is from \( t = 5 \) to \( t = 7 \), so the time spent during fusion is also \( 7 - 5 = 2 \) seconds.

However, the time during which each substance is being heated prior to the phase change is different, which affects the total heat absorbed by each. To calculate the heat absorbed for fusion alone (latent heat), we need to account for the heat absorbed during the temperature increase as well.

- For substance A: It takes 2 seconds to reach the fusion point, then 2 seconds to complete the fusion process.
- For substance B: It takes 3 seconds to reach the fusion point, then 2 seconds to complete the fusion.

Now, let's calculate the total heat absorbed for each substance:

\[
H_A = \text{Heat absorbed during heating phase} + \text{Heat absorbed during fusion}
\]

Substance A spends 2 seconds in the heating phase (at a rate of 6 cal/s), so it absorbs \( 2 \times 6 = 12 \) calories in the heating phase. For fusion, it absorbs heat for 2 seconds at the same rate:

\[
H_A = 12 + (2 \times 6) = 12 + 12 = 24 \, \text{cal}
\]

For substance B, it spends 3 seconds in the heating phase, absorbing \( 3 \times 6 = 18 \) calories. During the fusion, it also absorbs heat for 2 seconds:

\[
H_B = 18 + (2 \times 6) = 18 + 12 = 30 \, \text{cal}
\]

Now, the ratio of heat absorbed by substance A to substance B is:

\[
\frac{H_A}{H_B} = \frac{24}{30} = \frac{8}{5}
\]

Thus, the correct ratio of heat absorbed by substance A to substance B is indeed \(\frac{8}{5}\).