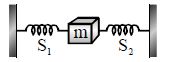
Solution:

Given that \( S_1 \) and \( S_2 \) are identical springs, they each have the same spring constant \( k \). When both springs are attached, they are in parallel, so the effective spring constant \( k_{\text{eq}} \) is:

\[
k_{\text{eq}} = k + k = 2k
\]

The frequency \( f \) of oscillation for mass \( m \) with effective spring constant \( k_{\text{eq}} = 2k \) is:

\[
f = \frac{1}{2\pi} \sqrt{\frac{2k}{m}}
\]

If One Spring is Removed

If one spring is removed, only one spring with constant \( k \) is left. The new frequency \( f' \) becomes:

\[
f' = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]

Ratio of New Frequency to Original Frequency

\[
\frac{f'}{f} = \frac{\frac{1}{2\pi} \sqrt{\frac{k}{m}}}{\frac{1}{2\pi} \sqrt{\frac{2k}{m}}} = \frac{\sqrt{\frac{k}{m}}}{\sqrt{\frac{2k}{m}}} = \frac{1}{\sqrt{2}}
\]

Thus:

\[
f' = \frac{f}{\sqrt{2}}
\]

Answer: \( f' = \frac{f}{\sqrt{2}} \)