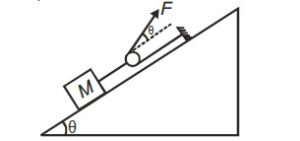
What is the minimum value of F needed so that block begins to move upward on frictionless incline plane as shown?
Solution:
🔹 Step-by-step:
- Block of mass M is on a frictionless incline of angle
- Force
is applied via a pulley system, split into two components:
- One acts up along the incline: F
- One acts horizontally, which when resolved along the incline becomes: F
Total upward force along incline =
Downward component of weight =
🔹 For the block to just start moving upward:
Now use the identity:
Final Answer:

Leave a Reply