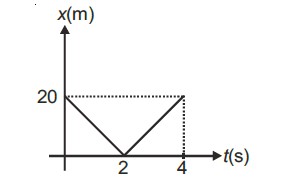
The position-time graph of a particle of mass 2 kg moving along x-axis is as shown in the figure. The magnitude of impulse on the particle at t = 2 s is
Solution:
Solution:
Impulse is given by the change in momentum:
From the graph, we find velocity before and after :
- Before :
- After :
Now, impulse:
Final Answer:


Leave a Reply