Solution:

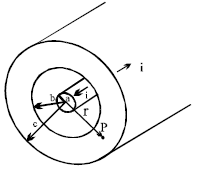
To calculate the magnetic field $B$ at a point $P$ within the outer shell of a coaxial cable ($b < r < c$), carrying equal and opposite currents $i$ on the inner and outer conductors, we use Ampère's law and superposition principles.

1. Current Distribution in the Outer Shell

The outer shell carries current $-i$, distributed uniformly across the cross-sectional area of the shell between radii $b$ and $c$.

The current density $J$ in the shell is:

$$J = \frac{-i}{\pi (c^2 - b^2)}.$$

The current enclosed within a radius $r$ ($b < r < c$) in the outer shell is the current $-i$ contributed by the region from $b$ to $r$:

$$I_{\text{enc,shell}} = J \cdot \text{area of shell portion} = J \cdot \pi (r^2 - b^2).$$

Substituting $J$:

$$I_{\text{enc,shell}} = \frac{-i}{\pi (c^2 - b^2)} \cdot \pi (r^2 - b^2) = \frac{-i (r^2 - b^2)}{c^2 - b^2}.$$

2. Net Enclosed Current at Radius $r$

At any point $P$ within the shell ($b < r < c$), the net current enclosed by a loop of radius $r$ is:

$$I_{\text{enc}} = \text{current from the inner wire} + \text{current from the outer shell}.$$

The inner wire contributes $+i$, and the shell contributes $I_{\text{enc,shell}}$:

$$I_{\text{enc}} = i + \frac{-i (r^2 - b^2)}{c^2 - b^2}.$$

Simplify:

$$I_{\text{enc}} = i \left(1 - \frac{r^2 - b^2}{c^2 - b^2}\right).$$

Factorize:

$$I_{\text{enc}} = i \cdot \frac{c^2 - r^2}{c^2 - b^2}.$$

3. Magnetic Field at Radius $r$

Using Ampère's law, the magnetic field $B$ at radius $r$ is:

$$B \cdot 2\pi r = \mu_0 I_{\text{enc}}.$$

Substitute $I_{\text{enc}}$:

$$B \cdot 2\pi r = \mu_0 \cdot i \cdot \frac{c^2 - r^2}{c^2 - b^2}.$$

Solve for $B$:

$$B = \frac{\mu_0 i}{2\pi r} \cdot \frac{c^2 - r^2}{c^2 - b^2}.$$

Final Answer:

$$\boxed{B = \frac{\mu_0 i}{2\pi r} \cdot \frac{c^2 - r^2}{c^2 - b^2}}$$