An isolated parallel-plate capacitor consists of two metal plates of area A and separation d. A slab of thickness t and dielectric constant K = 2 is inserted between the plates with its faces parallel to the plates and having the same surface area as that of the plates as shown (Fig.).
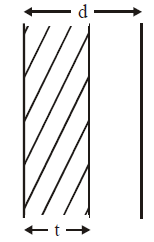
The capacitance of the system is :-
\[\frac{\varepsilon_{0}A}{\left( d-\frac{t}{2} \right)}\]
\[\frac{\varepsilon_{0}A}{\left( d+\frac{t}{2} \right)}\]
\[\frac{\varepsilon_{0}A}{d-t}\]
\[\frac{\varepsilon_{0}A}{d+t}\]
Solution:
The question involves calculating the capacitance of a parallel-plate capacitor when a dielectric slab of thickness and dielectric constant is partially inserted between the plates.
The short solution is based on treating the system as a combination of two capacitors in series:
- Capacitor 1 (region with dielectric): The thickness of this region is , and the capacitance is given by:
- Capacitor 2 (region without dielectric): The thickness of this region is , and the capacitance is:
Since the two regions are in series, the equivalent capacitance is given by:
Substituting and :
Simplifying:
Therefore:
When the dielectric slab thickness is , the capacitance simplifies to:
This matches the given answer. Let me know if further clarification is needed!
 The capacitance of the system is :-
The capacitance of the system is :-
Leave a Reply