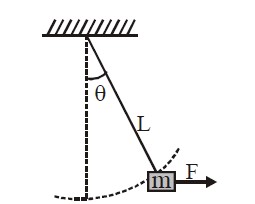
Solution:
Be definition of Work, Work Done = F.S. cos θ
Taking F and cos θ together like
W= (F. cos θ) . s = Component of Force along displacement × displacement
Here gravitational force mg is acting downwards and displacement in upward direction is (L- L cos θ), So
Work done = mg.(L-Lcosθ)cos (180°)= -mgL(1-cosθ)
Leave a Reply