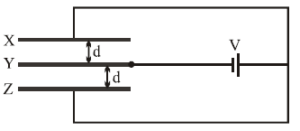
Consider the arrangement of three plates X, Y and Z each of area A and separation d. The energy stored in the system when the plates are fully charged is:
\[\frac{\varepsilon_{0}AV^{2}}{2d}\]
\[\frac{\varepsilon_{0}AV^{2}}{d}\]
\[\frac{2\varepsilon_{0}AV^{2}}{d}\]
\[\frac{3\varepsilon_{0}AV^{2}}{2d}\]
Solution:
To solve for the energy stored in the system of three plates (X, Y, Z), let's break the system into simpler components:
1. System Description
- The arrangement forms two capacitors:
- Capacitor 1: Between plates X and Y.
- Capacitor 2: Between plates Y and Z.
- Each capacitor has the same plate area and plate separation .
The capacitance of a parallel plate capacitor is given by:
Thus, the capacitance of each capacitor is:
2. Effective Capacitance
The two capacitors are in parallel because plate Y is connected to the battery on one side and plate X and Z are on the opposite side. For capacitors in parallel, the effective capacitance is:
3. Energy Stored in the System
The energy stored in a capacitor is:
Substitute :
Final Answer:
The energy stored in the system is:

Leave a Reply