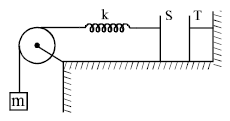
The plates S and T of an uncharged parallel plate capacitor are connected across a battery. The battery is then disconnected and the charged plates
are now connected in a system as shown in the figure. The system shown is in equilibrium. All the strings are insulating and massless. The magnitude of charge on one of the capacitor plates is: [Area of plates = A]
\[\sqrt{2mgA \epsilon_{0}}\]
\[\sqrt\frac{{4mgA \epsilon_{0}}}{k}\]
\[\sqrt{mgA \epsilon_{0}}\]
\[\sqrt\frac{{2mgA \epsilon_{0}}}{k}\]
Solution:
To solve this, let us analyze the situation and derive the required expression for the charge:
1. Setup of the System
- The parallel plate capacitor is initially charged, and the battery is disconnected.
- One plate of the capacitor is connected to a spring, and the other is attached to a mass .
- The capacitor plates attract each other due to the opposite charges, generating an electrostatic force.
2. Equilibrium Condition
In equilibrium, the upward force due to the spring's tension balances the downward gravitational force acting on the mass :
This tension is equal to the electrostatic force between the plates of the capacitor:
3. Force Balance
At equilibrium:
Substitute :
4. Solve for
Rearranging for :
Taking the square root:
Final Answer:
The magnitude of the charge on one of the capacitor plates is:

Leave a Reply