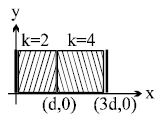
Solution:
Given Information:
- Parallel plate capacitor: Contains two dielectric layers.
- First layer () extends from to .
- Second layer () extends from to .
- Capacitor is connected to a battery: This means the potential difference across the plates is fixed.
Key Concepts:
- Electric Field in a Dielectric:
- The electric field in a dielectric is inversely proportional to the dielectric constant : where is the surface charge density.
- Continuity of Potential:
- Since the potential is constant across the capacitor, the sum of the potential drops across the two dielectric layers must equal . For a uniform electric field in each region: where and are the electric fields in the regions with and , respectively.
- Relation Between Fields:
- The electric displacement must be continuous across the boundary of the dielectrics: Substituting and , we find:
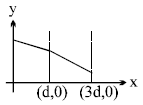
Explanation of the Graph:
- Region 1 ():
- In this region, the dielectric constant , so the electric field is relatively stronger compared to the next region.
- Region 2 ():
- Here, , and since , the electric field is halved.
Thus, the electric field decreases discontinuously at due to the change in the dielectric constant, leading to the stepwise graph shown in the second figure.
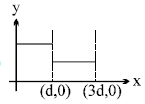
Leave a Reply