Rankers Physics
Topic: Capacitors
Subtopic: Capacitor With Dielectrics

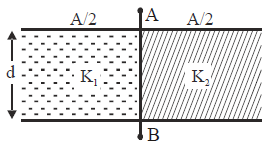
A parallel plate condenser is filled with two dielectrics as shown in figure. Area of each plate is A metre² and the separation is d metre. The dielectric constants are K1 and K2 respectively. Its capacitance in farad will be :       Image related to
\[\frac{\varepsilon_{0A}}{d}\left( K_{1} +K_{2}\right)\]
\[\frac{\varepsilon_{0A}}{d}\frac{\left( K_{1} +K_{2}\right)}{2}\]
\[\frac{\varepsilon_{0A}}{d}2\left( K_{1} +K_{2}\right)\]
\[\frac{\varepsilon_{0A}}{d}\frac{\left( K_{1} -K_{2}\right)}{2}\]

Solution:

Both the parts can be taken as separate capacitors connected in parallel.

So, C=C1+ C2=\(\frac{\varepsilon_{0A}}{d}\frac{\left( K_{1} +K_{2}\right)}{2}\)

Leave a Reply

Your email address will not be published. Required fields are marked *