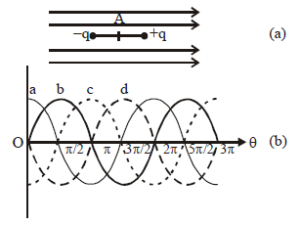
Solution:

For an electric dipole in a uniform electric field, the torque \( \tau \) on the dipole is given by:

\[
\tau = pE \sin \theta
\]

where:
- \( p \) is the dipole moment,
- \( E \) is the electric field strength,
- \( \theta \) is the angle between the dipole and the electric field.

Analysis:

1. Torque Variation:
- The torque \( \tau \) is maximum when \( \theta = \frac{\pi}{2}, \frac{3\pi}{2}, \dots \) (odd multiples of \( \frac{\pi}{2} \)), as \( \sin \theta = \pm 1 \).
- The torque \( \tau \) is zero when \( \theta = 0, \pi, 2\pi, \dots \), as \( \sin \theta = 0 \).

2. Graph Interpretation:
- The correct graph of \( \tau \) versus \( \theta \) will have positive and negative peaks at \( \theta = \frac{\pi}{2}, \frac{3\pi}{2}, \dots \), and cross zero at \( \theta = 0, \pi, 2\pi, \dots \).

Conclusion:

The correct answer is (b) as it represents the sinusoidal variation of torque with respect to \( \theta \) with alternating positive and negative values, matching the behavior of \( \tau = pE \sin \theta \).