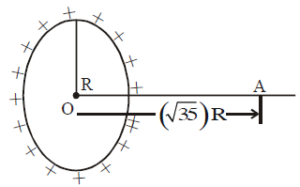
Solution:

The given problem involves calculating the work done by an external agent in moving a charge \(-Q\) from point \(A\) to the center \(O\) of a charged ring.

Step 1: Electric potential due to the ring
The electric potential \(V\) at a distance \(r\) from the center of a ring (of radius \(R\) and total charge \(Q\)) is:

\[
V(r) = \frac{kQ}{\sqrt{R^2 + r^2}}
\]

- At point \(A\) (\(r = \sqrt{35}R\)):

\[
V_A = \frac{kQ}{\sqrt{R^2 + (\sqrt{35}R)^2}} = \frac{kQ}{\sqrt{R^2 + 35R^2}} = \frac{kQ}{6R}
\]

- At the center \(O\) (\(r = 0\)):

\[
V_O = \frac{kQ}{R}
\]

---

Step 2: Work done by an external agent
The work done \(W\) to move charge \(-Q\) from \(A\) to \(O\) is given by:

\[
W = -q(V_O - V_A)
\]

Substituting \(q = -Q\), \(V_O = \frac{kQ}{R}\), and \(V_A = \frac{kQ}{6R}\):

\[
W = -(-Q) \left(\frac{kQ}{R} - \frac{kQ}{6R}\right)
\]

\[
W = Q \left(\frac{kQ}{R} - \frac{kQ}{6R}\right)
\]

\[
W = Q \cdot \frac{6kQ - kQ}{6R} = Q \cdot \frac{5kQ}{6R}
\]

\[
W = \frac{-5kQ^2}{6R}
\]

-------------------------------------------------------------------------------------------------------------------

Final Answer:
\[
{\frac{-5kQ^2}{6R}}
\]