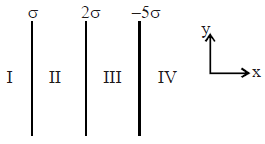
Solution:

The electric field due to an infinite sheet of charge with surface charge density \( \sigma \) is given by:

\[
E = \frac{\sigma}{2\epsilon_0}
\]

Now, let's determine the electric field in each region (I, II, III, and IV):

Region I:
Here, only the first sheet with charge density \( \sigma \) contributes. The field due to this sheet is:

\[
E_{\text{I}} = \frac{\sigma}{2\epsilon_0} \hat{i} + \frac{\sigma}{2\epsilon_0} \hat{i} = \frac{\sigma}{\epsilon_0} \hat{i}
\]

Region II:
In this region, both the first and second sheets contribute. The total electric field is:

\[
E_{\text{II}} = \left( \frac{\sigma}{2\epsilon_0} + \frac{2\sigma}{2\epsilon_0} \right) \hat{i} = \frac{2\sigma}{\epsilon_0} \hat{i}
\]

Region III:
Here, all three sheets contribute. The total field is:

\[
E_{\text{III}} = \left( \frac{\sigma}{2\epsilon_0} + \frac{2\sigma}{2\epsilon_0} + \frac{-5\sigma}{2\epsilon_0} \right) \hat{i} = \frac{4\sigma}{\epsilon_0} \hat{i}
\]

Region IV:
Only the third and fourth sheets contribute:

\[
E_{\text{IV}} = \left( \frac{-5\sigma}{2\epsilon_0} \right) \hat{i} = \frac{-\sigma}{\epsilon_0} \hat{i}
\]

Final Answers:
- Region I: \( \frac{\sigma}{\epsilon_0} \hat{i} \)
- Region II: \( \frac{2\sigma}{\epsilon_0} \hat{i} \)
- Region III: \( \frac{4\sigma}{\epsilon_0} \hat{i} \)
- Region IV: \( \frac{-\sigma}{\epsilon_0} \hat{i} \)