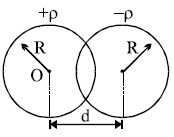
Solution:

To calculate the electric field in the overlap region, we use the principle of superposition of electric fields. Let's analyze:

Step 1: Electric field due to one sphere
For a uniformly charged non-conducting sphere, the electric field inside the sphere at a distance \(\vec{r}\) from the center is:

\[
\vec{E}_{\text{sphere}} = \frac{\rho}{3\epsilon_0} \vec{r}
\]

Here:
- \(\rho\) is the charge density of the sphere,
- \(\epsilon_0\) is the permittivity of free space,
- \(\vec{r}\) is the position vector from the center of the sphere.

Step 2: Contribution of both spheres in the overlap region
- For the positively charged sphere (\(+\rho\)), the electric field at any point in the overlap region is directed **away** from its center, proportional to \(\vec{r}_1\) (distance from its center).
- For the negatively charged sphere (\(-\rho\)), the electric field at any point in the overlap region is directed **toward** its center, proportional to \(\vec{r}_2\) (distance from its center).

Thus, the net electric field is the vector sum:

\[
\vec{E}_{\text{net}} = \frac{\rho}{3\epsilon_0} \vec{r}_1 + \frac{-\rho}{3\epsilon_0} \vec{r}_2
\]

Step 3: Relation between \(\vec{r}_1\), \(\vec{r}_2\), and \(\vec{d}\)
In the overlap region, \(\vec{r}_1 - \vec{r}_2 = \vec{d}\), where \(\vec{d}\) is the displacement vector between the centers of the two spheres.

Substitute this into the expression for \(\vec{E}_{\text{net}}\):

\[
\vec{E}_{\text{net}} = \frac{\rho}{3\epsilon_0} (\vec{r}_1 - \vec{r}_2) = \frac{\rho}{3\epsilon_0} \vec{d}
\]

Final Answer:

The electric field in the overlap region is:

\[
{\frac{\rho}{3\epsilon_0} \vec{d}}
\]