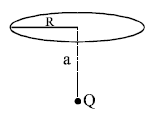
Solution:

To solve the problem using the formula:

\[
\Phi = \frac{Q}{2\varepsilon_0} \left(1 - \cos\theta\right),
\]

where \(\theta\) is the half-angle subtended by the disc at the charge, follow these steps:

1. The flux through the disc is given to be one-fourth of the total flux:
\[
\Phi = \frac{1}{4} \cdot \frac{Q}{\varepsilon_0}.
\]

Substituting this into the formula:
\[
\frac{1}{4} \cdot \frac{Q}{\varepsilon_0} = \frac{Q}{2\varepsilon_0} \left(1 - \cos\theta\right).
\]

2. Simplify:
\[
\frac{1}{4} = \frac{1}{2} \left(1 - \cos\theta\right).
\]

3. Multiply through by 2:
\[
\frac{1}{2} = 1 - \cos\theta.
\]

4. Solve for \(\cos\theta\):
\[
\cos\theta = 1 - \frac{1}{2} = \frac{1}{2}.
\]

5. Using the geometry, \(\cos\theta = \frac{a}{\sqrt{a^2 + R^2}}\). Substituting:
\[
\frac{a}{\sqrt{a^2 + R^2}} = \frac{1}{2}.
\]

6. Square both sides:
\[
\frac{a^2}{a^2 + R^2} = \frac{1}{4}.
\]

7. Rearrange:
\[
4a^2 = a^2 + R^2.
\]

\[
3a^2 = R^2.
\]

8. Solve for \(a\):
\[
a = \frac{R}{\sqrt{3}}.
\]

Thus, the relation is:

\[
a = \frac{R}{\sqrt{3}}.
\]