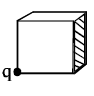
Solution:

To find the flux through the shaded face of the cube, we use symmetry:

1. The total flux through a closed surface is given by Gauss's law:
\[
\Phi_{\text{total}} = \frac{q}{\varepsilon_0}.
\]

2. The charge \(q\) is at one vertex of the cube. It is shared equally among 8 cubes because the vertex belongs to 8 adjacent cubes. Hence, the charge effectively enclosed in one cube is:
\[
q_{\text{enclosed}} = \frac{q}{8}.
\]

3. The flux through the entire surface of one cube is:
\[
\Phi_{\text{cube}} = \frac{q_{\text{enclosed}}}{\varepsilon_0} = \frac{q}{8\varepsilon_0}.
\]

4. A cube has 6 faces, and due to symmetry, the flux through each face is the same. Therefore, the flux through one face is:
\[
\Phi_{\text{one face}} = \frac{\Phi_{\text{cube}}}{6} = \frac{q}{48\varepsilon_0}.
\]

5. The shaded face is shared by 2 adjacent cubes, so it will receive twice the flux compared to one face:
\[
\Phi_{\text{shaded face}} = 2 \times \frac{q}{48\varepsilon_0} = \frac{q}{24\varepsilon_0}.
\]

Thus, the flux through the shaded face is:

\[
\Phi = \frac{q}{24\varepsilon_0}.
\]