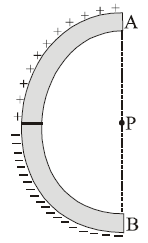
Solution:
Using the direct formula for the electric field due to a uniformly charged arc:
\[
E = \frac{2k\lambda \sin(\theta/2)}{r}
\]
Step 1: Identify Parameters
- \(\lambda\): Linear charge density.
- \(k = \frac{1}{4 \pi \varepsilon_0}\): Coulomb's constant.
- \(r\): Radius of the semicircle.
- \(\theta = \pi\): Angle subtended by the semicircle at the center.
Step 2: Substitute \(\lambda\)
The total charge on the semicircle is \(+Q\) or \(-Q\), and the arc length is \(\pi r\). Therefore:
\[
\lambda = \frac{Q}{\pi r}
\]
Step 3: Substitute into the Formula
\[
E = \frac{2k \lambda \sin(\pi/2)}{r}
\]
Here, \(\sin(\pi/2) = 1\). Substituting \(\lambda = \frac{Q}{\pi r}\):
\[
E = \frac{2k \left(\frac{Q}{\pi r}\right)}{r}
\]
Step 4: Simplify
\[
E = \frac{2k Q}{\pi r^2}
\]
Since \(k = \frac{1}{4 \pi \varepsilon_0}\), substitute \(k\):
\[
E = \frac{2}{4 \pi \varepsilon_0} \cdot \frac{Q}{\pi r^2}
\]
\[
E = \frac{Q}{\pi^2 \varepsilon_0 r^2}
\]
Final Answer:
The electric field at the center is:
\[
{\frac{Q}{\pi^2 \varepsilon_0 r^2}}
\]
Leave a Reply