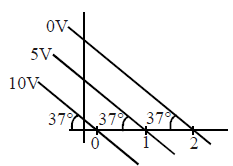
Solution:
To determine the electric field \(\vec{E}\) from the equipotential surfaces:
1. Electric Field Magnitude: The electric field is the negative gradient of the potential:
\[
|\vec{E}| = -\frac{\Delta V}{\Delta s}
\]
where \(\Delta V\) is the potential difference and \(\Delta s\) is the perpendicular spacing between equipotential surfaces.
2. Horizontal Component (\(E_x\)):
- The horizontal spacing between 0V and 10V surfaces is \(2 \, \text{units}\).
- \(E_x = -\frac{\Delta V_x}{\Delta x} = -\frac{10}{2} = -5 \, \text{V/unit}\).
3. Vertical Component (\(E_y\)):
- The vertical spacing between equipotential surfaces (tilted at \(37^\circ\)) corresponds to \(\tan 37^\circ = \frac{3}{4}\). Hence, the vertical spacing between 0V and 10V is \(2 \cdot \frac{3}{4} = 1.5 \, \text{units}\).
- \(E_y = -\frac{\Delta V_y}{\Delta y} = -\frac{10}{1.5} = -\frac{20}{3} \, \text{V/unit}\).
4. Resultant Electric Field:
\[
\vec{E} = -E_x \hat{i} - E_y \hat{j} = 5\hat{i} + \frac{20}{3}\hat{j}.
\]
Leave a Reply