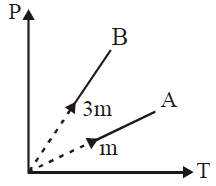
Solution:

To find the ratio of the slopes of curves \( B \) to \( A \) for gases with masses \( m \) and \( 3m \) at constant volume:

1. For an ideal gas at constant volume, \( P = \frac{nRT}{V} \).
2. Since \( n = \frac{\text{mass}}{\text{molar mass}} \), the pressure \( P \propto \frac{\text{mass} \cdot T}{M} \).
3. So, slope \( \propto \frac{\text{mass}}{M} \) for each gas.

For gas \( A \) with mass \( m \), let the slope be \( S \propto \frac{m}{M} \).
For gas \( B \) with mass \( 3m \), slope \( S_B \propto \frac{3m}{M} \).

Thus, the ratio of slopes \( \frac{S_B}{S_A} = \frac{3m/M}{m/M} = 3:1 \).