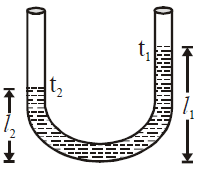
Solution:
For a liquid in a U-tube with different temperatures in each arm, the expansion of the liquid in each arm is affected by the temperature difference.
Let:
- \( l_1 \) and \( l_2 \) be the heights of the liquid columns at temperatures \( t_1 \) and \( t_2 \), respectively.
- \( \beta \) be the coefficient of volume expansion of the liquid.
Since the pressure at the same horizontal level in both arms must be equal, we have:
\[
l_1 (1 + \beta t_1) = l_2 (1 + \beta t_2)
\]
Rearranging, we get:
\[
l_1 + l_1 \beta t_1 = l_2 + l_2 \beta t_2
\]
Solving for \( \beta \):
\[
\beta = \frac{l_1 - l_2}{l_2 t_1 - l_1 t_2}
\]
Thus, the coefficient of volume expansion of the liquid is:
\[
\beta = \frac{l_1 - l_2}{l_2 t_1 - l_1 t_2}
\]
Leave a Reply